Mathematics at KS4

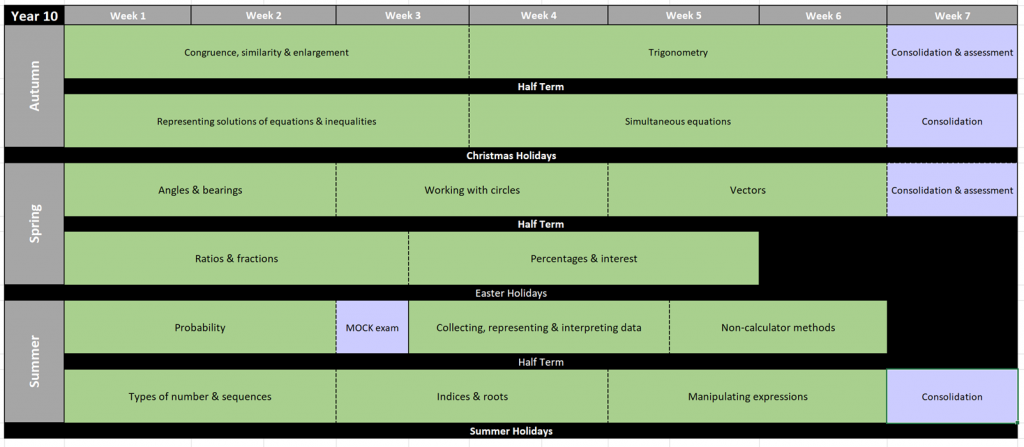
Year 11 Foundation Scheme of Learning

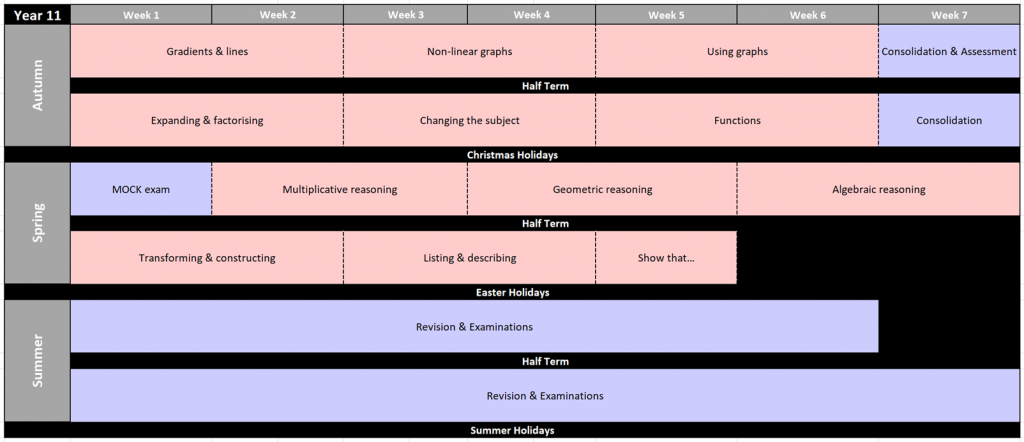
Year 11 Higher Scheme of Learning

Assessment and Feedback

At the end of each unit, pupils complete a low-stakes assessment allowing them to consolidate their learning and close any gaps in their knowledge. A more formal assessment takes place each term, based on the content they have been learning in lessons. Following these assessments, pupils receive an in-depth analysis, detailing their areas of strength and development. In year 10, homework is set weekly on an online platform called Sparx Maths. In year 11, pupils complete the online Sparx Maths homework one week and a past paper the following week.

Sparx Maths – Home

Useful Revision Websites

Pupils can revise for mathematics independently using the following websites which include videos, questions and answers:

Maths Genie – Free Online GCSE and A Level Maths Revision

Corbettmaths – Videos, worksheets, 5-a-day and much more

1st Class Maths – Free online GCSE Maths Revision

Extra-Curricular Activities

Each year, a selection of pupils from Key Stage 4 take part in the UK Intermediate Mathematical Challenge – a national competition aimed at promoting mathematical thinking and problem-solving skills. This prestigious challenge gives pupils the opportunity to apply their knowledge in unfamiliar and creative ways, competing against students from schools across the country. The highest-achieving participants are awarded bronze, silver, or gold certificates, recognising their success and celebrating their talent in mathematics. Taking part in the challenge is a valuable and enriching experience for our pupils, helping to develop their confidence and enthusiasm for the subject.

To support our Year 11 pupils in the lead-up to their GCSE examinations, we offer a range of targeted intervention opportunities. Pupils are invited to attend weekly after-school booster sessions, where they focus on their specific areas for development with support from subject specialists. We also hold Raising Achievement evenings, where students work through a variety of exam-style questions in a focused, supportive environment. These sessions are designed to strengthen understanding, build confidence, and help pupils develop effective exam techniques to maximise their success.

At our school, we offer the AQA GCSE Further Mathematics qualification as an additional opportunity for our higher attaining pupils. This course is designed to stretch and challenge students who demonstrate a strong aptitude for mathematics, providing them with the chance to explore more advanced mathematical concepts beyond the standard GCSE curriculum. Studying Further Mathematics helps to deepen their understanding and build confidence when tackling complex problems, while also giving them valuable preparation for A-Level Maths and related subjects. It is an excellent foundation for those considering pursuing mathematics or related fields at university or as part of a future career.

We also offer the Entry Level Certificate in Mathematics as an additional qualification to support our lower attaining pupils. This course is tailored to students who may find the full GCSE challenging, providing them with the opportunity to develop essential numeracy skills in a more accessible format. The Entry Level qualification allows students to experience success in maths, build their confidence, and gain a nationally recognised award that is valued by employers. It ensures that all learners leave school with a meaningful qualification that reflects their progress and supports their next steps in education or employment.